NumPy 使用¶
约 422 个字 200 行代码 2 张图片 预计阅读时间 4 分钟
介绍¶
数组对象:numpy.ndarray
参考资料
- GitHub - rougier/numpy-100: 100 numpy exercises (with solutions)
- NumPy的应用-1 - Python-100-Days
- NumPy 介绍
- GitHub - numpy/numpy-tutorials: NumPy tutorials & educational content in notebook format
np.argsort()
np.sort()
# 找到 2D 数组 arr 最小值的对应行、列索引
i, j = np.unravel_index(np.argmin(arr, axis=None), arr.shape)
# 数值积分函数;通过梯形法则(trapezoidal rule)计算定积分
np.trapz()
# 二维数组,按照第 2 列元素进行排序
array_sorted = array[array[:, 1].argsort()]
使用¶
工具¶
数组创建¶
初始化 numpy 数组时,可以进行预分配
import numpy as np
# 从列表创建数组
np.array([1, 2, 3]) # 一维
np.array([[1, 2], [3, 4]]) # 二维
# 从内置函数创建数组
np.eye() # 单位阵
np.zeros() # 全为 0
np.ones() # 全为 1
np.full() # 填充
np.diag() # 对角线
np.arange() # 范围(不包含终点值)
np.linspace() # 等差(默认包含终点值)
np.logspace() # 等比
np.fromstring() # 从字符串提取数据
# 创建随机数组
np.random.rand() # 0-1 随机小数
np.random.randint() # 随机整数
np.random.randn() # 标准正态分布随机数(均值为 0,标准差为 1)
np.random.normal() # 正态分布随机数
np.random.uniform() # 均匀分布随机数
# 数组元素是类浮点数的字符串时
a = [f"{x:.1f}" for x in range(1, 10)]
array = np.array(a, dtype=float)
属性¶
索引¶
普通索引、切片索引、布尔索引
arr[[1, 2], [1, 2]] # 索引的是 2 个元素,分别是 [1][1] 和 [2][2]
arr[np.ix_([1, 2], [1, 2])] # 索引的是子 2 维数组,即第 2、3 行与列的交叉数组
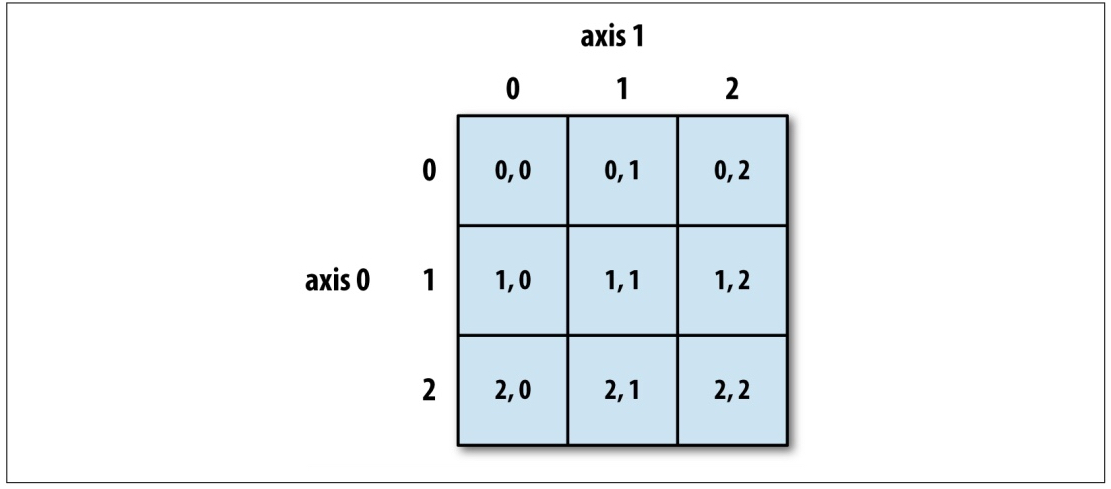
二维数组的普通索引
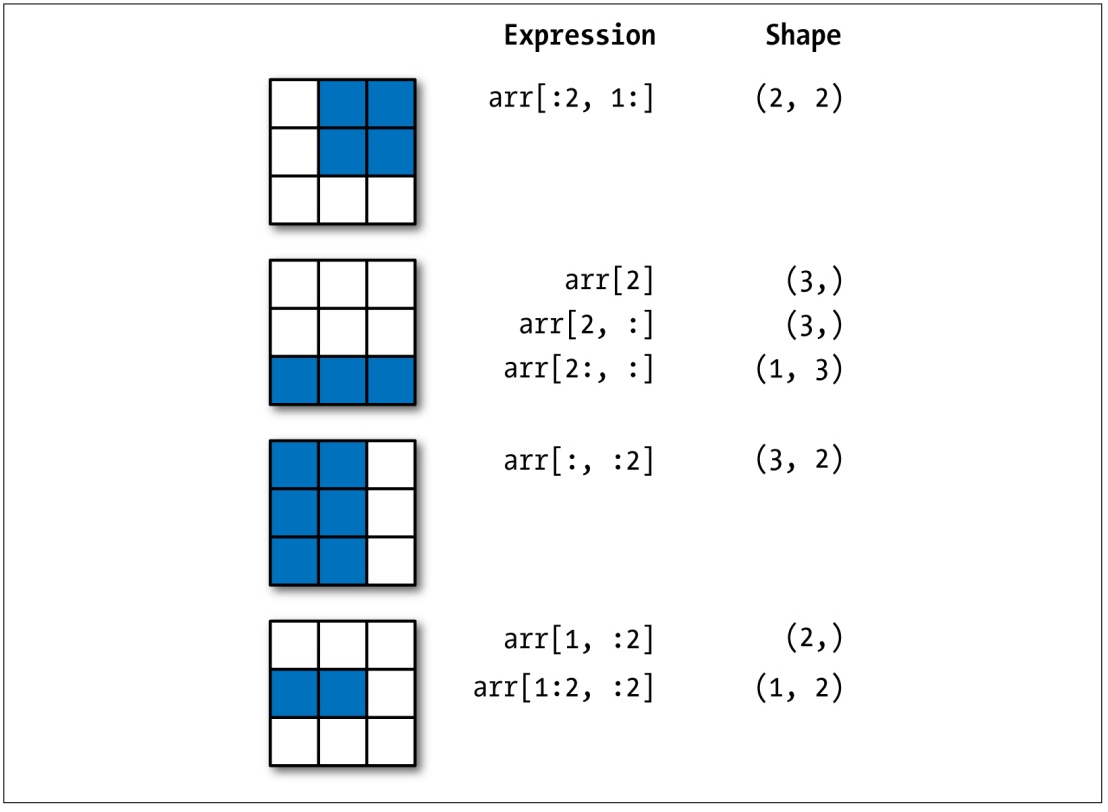
二维数组的切片索引
数学运算¶
* # 数组乘法,元素相乘
np.square() # 平方
np.sqrt() # 平方根
np.cbrt() # 立方根
np.log2() # 对数计算
np.round() # 保留小数位数
# 不使用科学计数法并指定精度
np.set_printoptions(precision=5, suppress=True)
通用一元函数:参数是一个数组对象,函数会对数组进行元素级的处理
abs / fabs # 绝对值
sqrt # 平方根
square # 平方
exp # e 指数幂
log / log10 / log2 # 对数函数
sign # 符号函数
ceil / floor # 向上/下取整
isnan # 返回布尔数组;NaN 为 True,非 NaN 为 False
isfinite / isinf # 判断数值是否为无穷大
cos / cosh / sin # 三角函数;其参数为弧度制
sinh / tan / tanh # 三角函数
arccos / arccosh / arcsin # 反三角函数
arcsinh / arctan / arctanh # 反三角函数
rint / round # 四舍五入
通用二元函数:参数是两个数组对象,函数会对两个数组中的对应元素进行运算
np.allclose(x, y) # 检查数组 x 和 y 元素是否几乎相等
np.dot(x, y) # 点积运算
np.inner(x, y) # 内积运算
np.cross(x, y) # 叉积运算
intersect1d(x, y) # 交集
统计¶
-
np.sum()、np.mean()等函数中的axis参数指定运算沿着哪一个轴来操作,axis=0为从上到下的方向进行,即对列进行操作,返回一维数组,尺寸为列数;axis=1为从左到右的方向进行,即对行进行操作,返回一维数组,尺寸为行数;不显式指定时为对整个数组,返回标量值 -
np.sort()、np.unique()等函数中不显式指定轴时,默认axis=-1,沿最后一个轴进行排序,若为二维数组,即在axis=1上进行操作
np.sum() # 加和
np.mean() # 算术平均值
np.min() # 最小值
np.max() # 最大值
np.std() # 标准差
np.var() # 方差
np.cumsum() # 累加和
其他常用函数¶
函数调用:
- 方式 1:Numpy 模块本身的函数(即 np.function()),如统计相关函数
- 方式 2:通过数组对象本身的方法(即 array.method()),如数组创建函数,数学和线性代数操作等
np.copy() # 拷贝
np.diff()
np.reshape() # 改变数组形状;当一个维度的参数值为 -1 时,会自动推断出该维度的值
tolist() # 转换成 list 类型
np.flatten() # 扁平化
np.unique() # 去重;返回的元素是排序过的(从小到大)
# 参数
return_count=True # 返回相同元素的数目
np.append() # 追加元素
np.insert() # 插入元素
np.where() # 条件查询
np.argwhere() # 满足条件的元素索引
np.where(array > 0.0) # 返回满足条件的数组元素索引
# 大于 0.0 保留原值,否则替换为 0.0
np.where(array > 0.0, array, 0.0)
np.all() # 判断数组是否所有元素都是 True
np.any() # 判断数组是否有为 True 的元素
np.hstack() # 横向堆叠多个数组构成新数组
np.vstack() # 纵向堆叠多个数组构成新数组
np.remainder() # 计算数组余数
np.isclose() # 比较两个数值是否在某个容忍范围内接近相等
# 参数
rtol # 相对容忍值
atol # 绝对容忍值
np.tril() # 提取下三角矩阵;参数 k 为对角线的偏移量(默认为 0)
np.triu() # 提取上三角矩阵
np.deg2rad() # 角度制转弧度制
np.rad2deg() # 弧度制转角度制
IO¶
-
查看 NumPy npy npz 格式文件的 VSCode 插件:vscode-numpy-viewer
-
npy、npz 格式区别:npy 只能存单个数组,npz 可存多个数组
np.save("*.npy", arr) # 存储到 npy 文件格式
np.savez("*.npz", ...) # 存储到 npz 文件格式
# 参数
*args # 位置参数,保存的数组将按顺序存储,名称为 arr_0 ...
**kwds # 关键字参数,给数组指定名称
# 用关键字参数将数组存储到 npz 文件
kwargs = {}
for i in range(3):
kwargs[f"array_{i}"] = ...
np.savez("*.npz", **kwargs)
np.load(file) # 导入 npy npz 文件
arr = np.load("*.npy")
data = np.load("*.npz")
data.files # 返回存储数组的名称列表
data["arr_0"]
np.dump() # 保存数组到二进制文件中
np.tofile() # 将数组写入文件中
np.savetxt()
np.loadtxt()
# 参数
skiprows
use_cols # 指定列数据
# 从普通文本中读取数据
np.genfromtxt()
线性代数¶
linalg 模块
.T # 转置
np.transpose() # 同上
@ # 矩阵乘法
np.matmul() # 同上
np.dot() # 矩阵 1D,点积;2D,矩阵相乘
np.inner # 内积
np.outer() # 1*n 一维列向量与 m*1 一维行向量外积得到 m*n 矩阵
np.triu(..., k=...) # 提取上三角矩阵;k 为偏移量
np.linalg.trace() # 对角线元素和
np.linalg.matrix_rank() # 矩阵的秩
np.linalg.inv() # 求逆
np.linalg.pinv() # 伪逆(非方阵或奇异矩阵)
np.linalg.det() # 求行列式
np.linalg.eig() # 计算特征值、特征向量
np.linalg.qr() # QR 分解
np.linalg.svd() # 奇异值分解
np.linalg.solve() # 解线性方程组
np.linalg.norm(x, ord="fro") # 范数 ord="fro" F-范数